Nyligen i Superbloggen skrev jag ytterligare två inlägg om datorer och spel, här om limitpoker…

https://bloggar.aftonbladet.se/superbloggen/2015/01/datorn-1-manniskan-0-i-poker/

… och här om schack:

https://bloggar.aftonbladet.se/superbloggen/2015/01/det-forsta-steget/

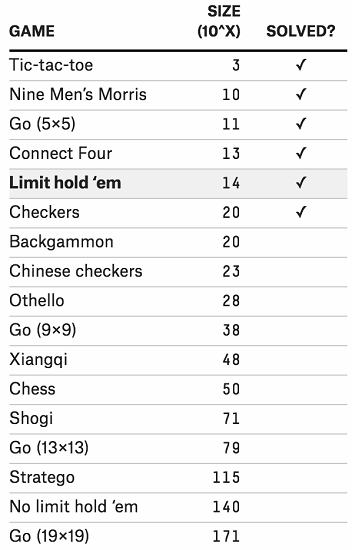
Var står vi egentligen när det gäller att ”knäcka” olika spel? Och då i betydelsen att med datorernas hjälp komplett analysera samtliga möjliga existerande positioner och situationer som kan uppkomma, för att på så sätt få fram den vinnande strategin – eller som till exempel i fallet damspel en strategi som garanterat inte kan förlora, eftersom det blir remi med optimalt spel från bägge sidor. Här är en liten lista:

Bilden visar komplexiteten i ett antal vanliga spel, mätt i vad som på analysspråk kallas för ”state space”: alltså hur många olika möjliga positioner/situationer som kan uppstå i spelet, i runda tal. (I fallen med poker och kinaschack avses spel heads-up; alla de andra spelen är också för två deltagare.) För tripp-trapp-trull finns i storleksordningen 1000 olika positioner, alltså en 1:a följd av tre nollor; för kvarn (nine men’s morris) finns 10 miljarder olika positioner, alltså en 1:a följd av tio nollor; och så vidare nedåt i listan. Som jämförelse uppskattas antalet vattenmolekyler i världshaven på vår planet vara en 1:a följd av 49 nollor, och antalet atomer i hela Universum till en 1:a följd av 80 nollor.

Ett spel som av någon anledning saknas i listan ovan är för övrigt kalaha/mancala, som i sin internationella tävlingsversion oware (samt några andra varianter) knäcktes år 2000 av ett kombinerat forskarteam från universitetet i Maastricht i Nederländerna och universitetet i Pasadena i Kalifornien: ett ”state space” bestående av en 1:a följd av 12 nollor, och med perfekt strategi resulterande i antingen remi eller vinst för den förste spelaren, beroende på variant. Här är deras rapport om du intresserar dig för den:

https://naml.us/~irving/papers/irving2000_kalah.pdf

Vad bestämmer då om spel är lätt eller svårt att lösa med datorernas hjälp? Jo, i huvudsak just måttet på hur ”stort” det är, uttryckt som ”state space”.

Forskarna har gradvis arbetat sig nedåt i listan. Tripp-trapp-trull analyserades tack vare sin enkelhet redan i datorernas barndom, fyra-i-rad 1988, kvarn 1993 och så vidare. Damspelet tog fram till 2007 och är det hittills mest komplexa spelet som knäckts; och limitpoker heads-up löstes nu i januari 2015, som du kunnat läsa om i ett inlägg av mig här i Superbloggen.

Och vad kommer att hända härnäst? Att knäcka schack – även om datorerna redan är bättre än människan i det spelet – samt därefter go (där de bästa programmen än så länge inte spelar bättre än ”på kompetent nivå”) är vetenskapens heliga graal inom det området, men det är osannolikt att det inträffar under min och er läsares livstid. Hur bra teknologin än blir, och även om vi får ett genombrott inom till exempel kvantdatorforskningen, är Universum konstruerat så att det faktiskt existerar fysikaliska gränser vi inte kan överskrida: ljushastigheten, kvantbarriären och den termodynamiska barriären, vilka alla på ena eller andra sättet i en avlägsen framtid kommer att sätta de ultimativa gränserna för datorernas kapacitet. ”Enligt vad vi hittills vet”, bör dock försiktigtvis tilläggas – som alltid när det gäller vetenskapen och dess rön.

Och frågan infinner sig också: varför plöja ner miljontals dollar och oräkneliga arbetstimmar på att hålla på att knäcka olika spel?

Svaret är tvåfaldigt. Dels dras vi människor till utmaningar; det räcker med att påminna om Edmund Hillarys klassiska svar om varför han tillsammans med Norgay Tenzing valde att som de två första någonsin bestiga Mount Everest – ”because it’s there”. Men dels har också det forskningsarbete som lagts ner på metodiken i själva problemlösandet när det gäller spel, i form av nya algoritmer och analysmetoder, redan burit oväntad frukt i form av resultat som visat sig applicerbara inom till exempel cancer- och diabetesforskning. Så vem vet vilka nya spelgenombrott vi står inför de närmaste 10 eller 20 åren?