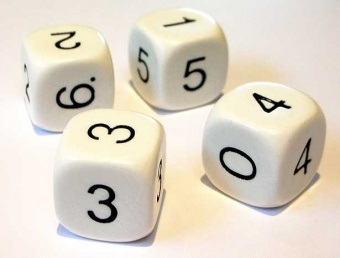Det finns en del udda fenomen inom tärningsmatematik. Kanske minns du när jag här i Superbloggen föreslog att du skulle spela backgammon med Sicherman-tärningar, för en udda upplevelse:

https://bloggar.aftonbladet.se/superbloggen/2013/09/backgammon-sicherman-style/

Nu har det blivit dags för mig att utmana dig på ett tärningsspel: varsågod, välj en av dessa tärningar, vilken du vill!

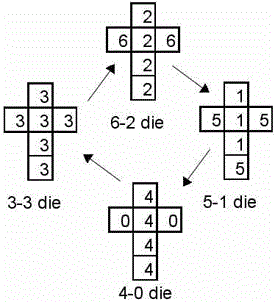
Om du är nyfiken, så är numreringen på de olika sidorna 6-6-2-2-2-2 (tärning A) resp 5-5-5-1-1-1 (B) resp 4-4-4-4-0-0 (C) resp 3-3-3-3-3-3 (tärning D). Efter att du valt, så kommer jag att välja en av de återstående tärningarna… och så slår vi och ser vem som får högst. För att utjämna slumpen bestämmer vi till och med att vi slår flera gånger om: först till låt oss säga 10 vinster har segrat. Vi sätter väl en krona eller två var också, för att göra det lite mera spännande?

Resultatet? You are dead meat, baby.

Välkommen till den udda värld som befolkas av icke-transitiva tärningar.

Om du gör matematiken och jämför alla de möjliga utfallen, kommer du att se att i det långa loppet vinner tärning A över tärning B, två gånger av tre (av de 36 möjliga kombinationerna i kastet, 6×6, mellan dessa två vinner tärning A hela 24 gånger men tärning B bara 12 gånger).

Jämför på samma sätt tärning B mot tärning C… och du kommer att se att B vinner över C med samma 24-12 i olika möjliga resultat!

Nå, tärning C mot tärning D då? Du gissade rätt: 24-12, till tärning C:s fördel.

Och tärning D mot tärning A, till slut? Resultatet av de 36 möjliga kasten, alla med samma sannolikhet att inträffa, blir… 24-12, till D:s fördel.

Så här fungerar det:

Vänta ett tag! ropar du säkert. Det är omöjligt! Om Adam i klassen är längre än Bertil som är längre än Charlie som är längre än David, kan David definitivt INTE vara längre än Adam!

Och just den detaljen stämmer ju, förstås – men välkommen som sagt till en av spelmatematikens kuriositeter slash paradoxer, och med paralleller till sten-sax-och-påse. Oavsett vilken tärning du väljer ovan, kan jag alltså följaktligen välja en annan som besegrar dig i det långa loppet, och därmed plocka dig som en kyckling. Ja, det må framstå som hur kontraintuitivt som helst, men icke desto mindre är det en matematisk realitet.

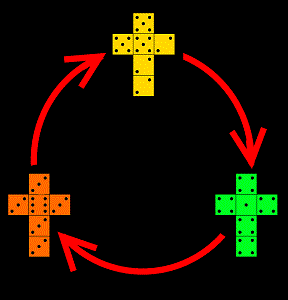
Fenomenet icke-transitiva tärningar är känt sedan omkring 1970; och exemplet ovan är inte det enda, på långa vägar. Här är en variant med tre tärningar:

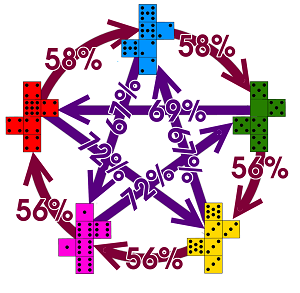
Går ”knepet” att göra med fler än fyra tärningar då? Javisst – här är en uppsättning av fem så kallade Grime Dice:

Intressant nog kan Grime-tärningar användas för att simulera valprocesser i ett system med fem politiska partier, när de slås alla samtidigt – men det är ett ämne som skulle föra alltför långt utanför detta inlägg.

Att känna till fenomenet med icke-transitiva tärningar kan vara kul, och göra så att du sparar pengar den gång i framtiden som någon främling vid sidan om dig plockar upp en liten grupp tärningar med udda utseende ur fickan och föreslår ”a friendly game”.

En känd fan av icke-transitiva tärningar är finansmagnaten Warren Buffett. I boken ”Fortune’s Formula: The Untold Story of the Scientific Betting System that Beat the Casinos and Wall Street” återges en diskussion mellan Buffett och Edward Thorp – den man som “knäckte” blackjack på 1960-talet – i just det ämnet. Buffett sägs också en gång ha försökt lura in Bill Gates i ett highstakesparti med icke-transitiva tärningar; men efter att Gates hade inspekterat alla tärningarna, krävde han att Buffett i stället skulle välja först!